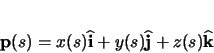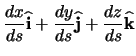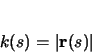Next: Straight Elements
Up: Geometry
Previous: Geometry
Contents
Elements
For this study, a roller coaster track will be modeled as a set of elements, aligned such that one
begins where the previous one ended. In order to connect these elements to create a track, as
well as to accurately model the dynamics, many geometric quantities must be known everywhere
along the track. This section will introduce these quantities and explain the general derivation
techniques for many of them. It will also explain the techniques used to guarantee curvature
continuity throughout the track.
Many of the geometric parameters that need to be known vary from one element to the next, and
will be discussed in sections 2.1.1-2.1.5; however, the following quantities must be
known for all elements.
- Geometric Parameters
- length

- The arclength of the element. This may also be denoted as
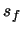 .
.
- vertical angle
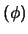
- The vertical angle is the angle between the forward
direction and the
 -
-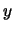 plane. Refer to figure 1.4. The initial and final vertical
angles, denoted as
plane. Refer to figure 1.4. The initial and final vertical
angles, denoted as 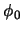 and
and  , will need to be determined.
, will need to be determined.
- azimuth angle

- The azimuth angle is the angle between the projection of
the forward direction in the
 -
-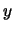 plane and the
plane and the  axis. Refer again to figure
1.4. The element will be created such that the initial azimuth angle is zero. The
final angle,
axis. Refer again to figure
1.4. The element will be created such that the initial azimuth angle is zero. The
final angle,  , will need to be determined.
, will need to be determined.
Other quantitites that must be determined along the track are functions of the distance into the
element,  . These include the following.
. These include the following.
- Geometric Functions
- position vector (
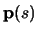 )
)
- The coordinates of every point along the
element must be determined.
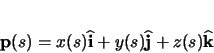 |
(2.1) |
- forward vector (
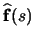 )
)
- The forward vector at any point along the element must be known. This is tangent to the track, and is defined as the derivative of the position vector with respect to arclength. Note that the result is a unit vector.
- radial vector (
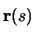 )
)
- This is a vector pointing toward the center of curvature. It is defined as the second derivative of the position vector with respect to arclength, which is the same as the first derivative of the forward vector with respect to arclength.
The unit radial vector is now determined.
- curvature (
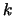 )
)
- The curvature of the track is the magnitude of the (non-unit) radial
vector.
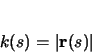 |
(2.4) |
The following sections describe in detail how the above quantities are determined. In order to make it easier for the reader to find essential information quickly, the equations describing the required geometric parameters and functions will be numbered as they are calculated in sections 2.1.1-2.1.5.
The curvature at the ends of each element is zero, in order to guarantee curvature continuity throughout the track. Since the middle of an element may have non-zero curvature, a shape must be
used to connect the zero curvature region with the non-zero curvature region. This shape is a
clothoid,2.1 a geometric entity that has linearly varying curvature with respect to distance along
the curve. Clothoids are used in all elements discussed here, except straight elements. All
elements at least partially composed of a clothoid will be referred to as clothoidal
elements. Clothoids allow curvature continuity to be maintained throughout elements with
varying curvature. A clothoidal element is made up of three sections:
- entrance clothoid
- The region in which the curvature varies linearly from
zero to some maximum value.
- circular region
- The region in which the curvature remains constant.
- exit clothoid
- The region in which the curvature varies linearly from the
maximum value back to zero.
The entrance clothoid region is referred to as clothoid 1, and all parameters related to it are
subscripted 1. The exit clothoid is referred to as clothoid 2, and its parameters are
subscripted 2. Thus, each clothoidal element is made up of clothoid 1, a circular region, and
clothoid 2.
A special note should be made about how the geometry of the three-dimensional elements (the curve, loop, and corkscrew) is created. The circular and clothoidal regions of an element are initially created in a plane. (This is the  -
-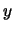 plane for the curve and the
plane for the curve and the  -
- plane for the loop and corkscrew.) The element is then stretched along the axis perpendicular to the plane of creation, (the
plane for the loop and corkscrew.) The element is then stretched along the axis perpendicular to the plane of creation, (the  direction for curves and the
direction for curves and the 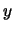 direction for loops and corkscrews), such that the position change in this direction is linear with respect to distance along the element. This results in a constant angle between the plane of creation of the element and the tangent to the element after it has been stretched. This angle will be referred to as the vertical angle,
direction for loops and corkscrews), such that the position change in this direction is linear with respect to distance along the element. This results in a constant angle between the plane of creation of the element and the tangent to the element after it has been stretched. This angle will be referred to as the vertical angle, 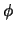 , for the curve, and the shift angle,
, for the curve, and the shift angle, 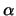 , for the loop and the corkscrew.
, for the loop and the corkscrew.
This approach of ``linear stretching'' may be considered somewhat simplistic when compared with the alternate method of allowing any desired curvature variations. However, as will be seen in the following sections, maintaining curvature continuity throughout the elements, even the two-dimensional joint, is a very complex process. This technique of transitioning from two to three-dimensions was used in order to prevent the creation of the these elements from becoming excessively complex. In this way, the goal of curvature continuity is maintained, while enabling the flexibility to create three-dimensional elements.
2.1
See appendix A for a complete discussion of clothoids.
Subsections




Next: Straight Elements
Up: Geometry
Previous: Geometry
Contents
Darla Weiss
2000-02-13

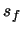 .
.
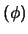
 -
-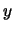 plane. Refer to figure 1.4. The initial and final vertical
angles, denoted as
plane. Refer to figure 1.4. The initial and final vertical
angles, denoted as 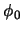 and
and  , will need to be determined.
, will need to be determined.

 -
-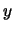 plane and the
plane and the  axis. Refer again to figure
1.4. The element will be created such that the initial azimuth angle is zero. The
final angle,
axis. Refer again to figure
1.4. The element will be created such that the initial azimuth angle is zero. The
final angle,  , will need to be determined.
, will need to be determined.