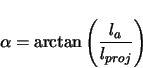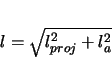Next: Back to the Corkscrew...
Up: Corkscrew Elements
Previous: Corkscrew Elements
Contents
The central axis length of the corkscrew is similar to the shift angle of the loop or the vertical angle of a curve. It is the direction the corkscrew is ``linearly stretched'' along to create the three-dimensional element. The distance along the central axis varies linearly with the arclength along the corkscrew.
Let 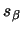 represent the projected arclength in the
represent the projected arclength in the  -
- plane of the corkscrew from
plane of the corkscrew from 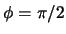 to
to 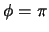 . Let
. Let 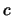 represent the length along the axis over the same range of
represent the length along the axis over the same range of 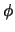 . Refer to figure 2.7. Since the axis length varies linearly as the arclength along the corkscrew, and therefore varies linearly as the projected arclength along the corkscrew,2.7 the following can be shown.
. Refer to figure 2.7. Since the axis length varies linearly as the arclength along the corkscrew, and therefore varies linearly as the projected arclength along the corkscrew,2.7 the following can be shown.
The range of 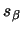 is entirely within the circular region of the corkscrew. Its projected
arclength in the
is entirely within the circular region of the corkscrew. Its projected
arclength in the  -
- plane can therefore be determined from the following.
plane can therefore be determined from the following.
From the figure a relationship can be found for 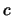 in terms of
in terms of 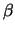 .
.
Making substitutions from above determines the total axis length.
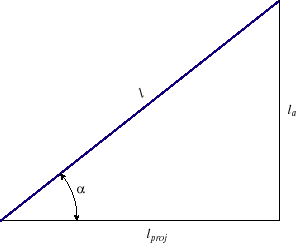
Figure 2.8: Corkscrew Shift Angle.
This figure illustrates the relationship between the total length of the corkscrew, the length of the projection in the
 -
- plane, and the axis length. Note that
plane, and the axis length. Note that
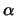 is a constant angle throughout the corkscrew, as explained in section 2.1.
is a constant angle throughout the corkscrew, as explained in section 2.1.
|
The shift angle of a corkscrew, 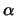 , is analogous to that of a loop. Figure
2.8 depicts the arclength of the corkscrew as the hypotenuse of the triangle,
while the lower leg represents the projected length in the
, is analogous to that of a loop. Figure
2.8 depicts the arclength of the corkscrew as the hypotenuse of the triangle,
while the lower leg represents the projected length in the  -
- plane. The length of the axis is
the length of the right leg.
plane. The length of the axis is
the length of the right leg.
The arclength of the corkscrew is given by the Pythagorean Theorem.
2.7
Refer to figure 2.8. Since the angle 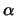 is constant, as discussed in section 2.1, this is a true statement.
is constant, as discussed in section 2.1, this is a true statement.




Next: Back to the Corkscrew...
Up: Corkscrew Elements
Previous: Corkscrew Elements
Contents
Darla Weiss
2000-02-13
![]() represent the projected arclength in the
represent the projected arclength in the ![]() -
-![]() plane of the corkscrew from
plane of the corkscrew from ![]() to
to ![]() . Let
. Let ![]() represent the length along the axis over the same range of
represent the length along the axis over the same range of ![]() . Refer to figure 2.7. Since the axis length varies linearly as the arclength along the corkscrew, and therefore varies linearly as the projected arclength along the corkscrew,2.7 the following can be shown.
. Refer to figure 2.7. Since the axis length varies linearly as the arclength along the corkscrew, and therefore varies linearly as the projected arclength along the corkscrew,2.7 the following can be shown.
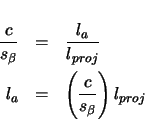
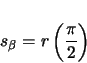



![]() , is analogous to that of a loop. Figure
2.8 depicts the arclength of the corkscrew as the hypotenuse of the triangle,
while the lower leg represents the projected length in the
, is analogous to that of a loop. Figure
2.8 depicts the arclength of the corkscrew as the hypotenuse of the triangle,
while the lower leg represents the projected length in the ![]() -
-![]() plane. The length of the axis is
the length of the right leg.
plane. The length of the axis is
the length of the right leg.