This figure shows the geometric shape known as a clothoid, whose curvature varies linearly with distance along the curve.

A clothoid is a curve with linearly varying curvature. Since the intention of this research is to create a track with continuous curvature, clothoids are used extensively. An illustration of a clothoid is shown in figure A.1

|
The position of points along a clothoid is evaluated with the use of the Fresnel Integrals, shown below:
 |
(A.1) | ||
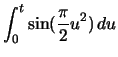 |
(A.2) |
These integrals cannot be solved analytically. Algorithms, as well as C code, have been created to evaluate the Fresnel Integrals[14].
The equations of a clothoid are:
| (A.3) | |||
| (A.4) |
In the above, ![]() is a scaling parameter and
is a scaling parameter and ![]() is the implicit variable, in general ranging from zero to
is the implicit variable, in general ranging from zero to ![]() . The range of
. The range of ![]() determines the variation of curvature within the clothoid, as well as the initial and final tangent angles.
determines the variation of curvature within the clothoid, as well as the initial and final tangent angles.
Some useful parameters of clothoids are given below[15].
In the methodology being used, the clothoid will always have zero curvature and zero tangent angle at one end, with a specified radius ![]() and angle
and angle ![]() at the other end. The parameter
at the other end. The parameter ![]() and the range of
and the range of ![]() can be found using these specified values.
can be found using these specified values.
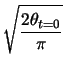 |
|||
| (A.8) |
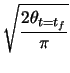 |
|||
| (A.9) |
| (A.10) | |||
| (A.11) |
The arclength of the clothoid can now be calculated.
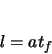 |
(A.12) |