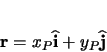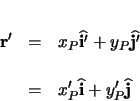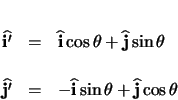Rotation Transformations

Many calculations of a roller coaster track require performing a rotation of a specified angle about a specified axis, as shown in figure B.1. It is desirable to know the location of the points in the rotated frame in terms of the unit vectors describing the non-rotated frame. This appendix will illustrate the calculation performed.

Figure B.1: Rotation Transformations.
This figure illustrates the rotation of the position vector 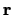$\mathbf{r}$ through a specified angle $\theta$.

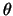Let point 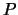$P$ be specified in the 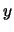$x$-$y$ coordinate system by the vector $\mathbf{r}$.

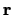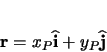$$\mathbf{r} = x_{P} \ensuremath \mathbf{\widehat{i}} + y_{P} \ensuremath \mathbf{\widehat{j}}$$ (B.1)

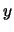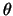The $x$-$y$ axes are then rotated about the $z$ axis through an angle $\theta$, resulting in the 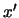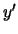$x'$-$y'$ axes. Point 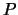$P$ is rotated as well, producing point 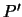$P'$ and position vector 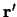$\mathbf{r'}$, which can be represented two ways.

$$\begin{eqnarray*} \mathbf{r'} & = & x_{P} \ensuremath \mathbf{\widehat{i'}} + y... ...h \mathbf{\widehat{i}} + y_{P}' \ensuremath \mathbf{\widehat{j}} \end{eqnarray*}$$

From the figure, it can be seen that:

$$\begin{eqnarray*} \ensuremath \mathbf{\widehat{i'}} & = & \ensuremath \mathbf{\... ...hat{i}} \sin\theta + \ensuremath \mathbf{\widehat{j}} \cos\theta \end{eqnarray*}$$

The new position vector, 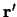$\mathbf{r'}$, can now be written as:

$$\mathbf{r'} = x_{P} ( \ensuremath \mathbf{\widehat{i}} \cos... ...i}} \sin\theta + \ensuremath \mathbf{\widehat{j}} \cos\theta )$$

The new coordinates can now be written in terms of the non-rotated axes.

$$x_{P}' = x_{P} \cos\theta - y_{P} \sin\theta$$ (B.2)

$$y_{P}' = x_{P} \sin\theta + y_{P} \cos\theta$$ (B.3)