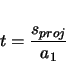
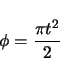
The projection of the loop in the ![]() -
-![]() plane is determined by the Fresnel Integrals.
The
plane is determined by the Fresnel Integrals.
The ![]() coordinate varies linearly with the arclength of the loop.
coordinate varies linearly with the arclength of the loop.
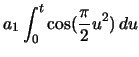 |
(2.53) | ||
| (2.54) | |||
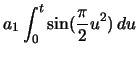 |
(2.55) |
The calculation of the forward and radial vectors is nearly identical to the calculation in the curve. An abbreviated description will be shown here.
Derivatives with respect to arclength of the position vector must be taken. The required chain rule relationships are first determined.
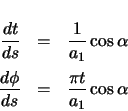
The forward vector is calculated as the derivative of the position vector with respect to arclength.
![$\displaystyle \ensuremath \frac{d\left[ a_{1} \ensuremath\int_{0}^{t} \cos(\frac{\pi}{2} u^{2})\,du \right]}{dt} \ensuremath \frac{dt}{ds}$](img141.gif) |
|||
| (2.56) | |||
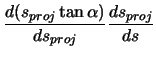 |
|||
| (2.57) | |||
![$\displaystyle \ensuremath \frac{d\left[ a_{1} \ensuremath\int_{0}^{t} \sin(\frac{\pi}{2} u^{2})\,du \right]}{dt} \ensuremath \frac{dt}{ds}$](img145.gif) |
|||
| (2.58) |
The radial vector is calculated as the derivative of the forward vector with respect to arclength.
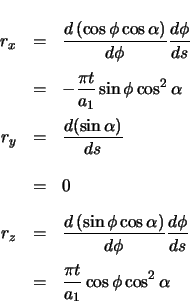
| (2.59) | |||
| (2.60) | |||
| (2.61) |
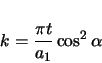 |
(2.62) |