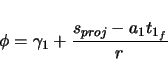
The end of the first clothoid occurs when ![]() . The position at
. The position at ![]() is found, and the center of the circular region is determined from it. This point,
is found, and the center of the circular region is determined from it. This point,
![]() , can be seen in figure 2.5.
, can be seen in figure 2.5.
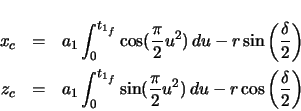
| (2.63) | |||
| (2.64) | |||
| (2.65) |
Derivatives with respect to arclength will need to be taken to determine the remaining functions.
Since the position vector is expressed in terms of ![]() , the chain rule is applied.
, the chain rule is applied.
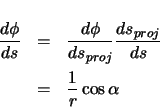
The forward vector is calculated as the derivative of the position vector with respect to
arclength.
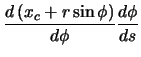 |
|||
| (2.66) | |||
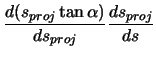 |
|||
| (2.67) | |||
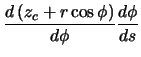 |
|||
| (2.68) |
The radial vector is calculated as the derivative of the forward vector with respect to arclength.
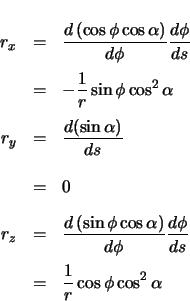
| (2.69) | |||
| (2.70) | |||
| (2.71) |
 |
(2.72) |