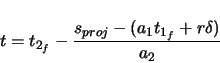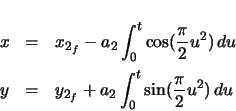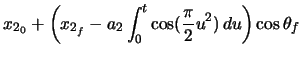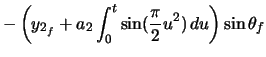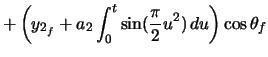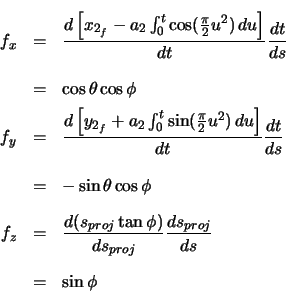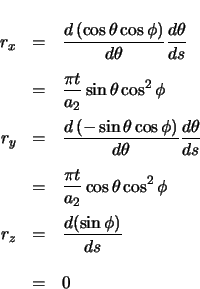Next: Loop Elements
Up: Curve Elements
Previous: Circular Region:
Contents
The coordinates at the beginning of clothoid 2 are found from the coordinates of the center of the
curve.
The end of the curve element has zero curvature. Since clothoids have zero curvature when 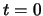 , clothoid 2 must end with
, clothoid 2 must end with 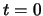 , and therefore begin at
, and therefore begin at 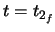 , with non-zero curvature. The range of
, with non-zero curvature. The range of 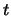 is depicted in figure 2.4.
is depicted in figure 2.4.
Clothoid 2 is initially created ending at horizontal, as seen in the figure. The azimuth angle along the clothoid is found from the value of 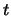 given above and from equation A.7.
given above and from equation A.7.
The location of the end of the clothoid is calculated,
 , and can be seen in the figure after the clothoid's translation to begin at its starting point,
, and can be seen in the figure after the clothoid's translation to begin at its starting point,
 .
.
The coordinates of all points along the clothoid are then calculated from the endpoint of the
clothoid,
 .
.
The clothoid is then rotated  radians about the
radians about the  axis to line up the azimuth angle at the beginning of clothoid 2 with the angle at the end of the circular region. Appendix B discusses rotation transformations in detail. Clothoid 2 is translated to begin at
axis to line up the azimuth angle at the beginning of clothoid 2 with the angle at the end of the circular region. Appendix B discusses rotation transformations in detail. Clothoid 2 is translated to begin at
 after the rotation is complete.
after the rotation is complete.
The calculation of the forward and radial vectors can be performed in two ways. The derivatives
of the final position vector with respect to arclength may be taken, or the derivative may be taken
before the rotation is made. The forward and radial vectors would then be rotated. The second
approach will be used here.
The calculation of the derivatives is nearly identical to the calculation in clothoid 1. An
abbreviated description will be shown here.
The required chain rule relationships are first determined.
The forward vector is initially determined as the derivative with respect to arclength of the
position vector before it is rotated.
This vector will now be rotated  radians about the
radians about the  axis.
axis.
The radial vector is initially determined as the derivative of the forward vector with respect to
arclength, before its rotation.
The unit vector in the direction of the radial vector must be determined.
This vector will now be rotated  radians about the
radians about the  axis.
axis.
The curvature is the magnitude of the (non-unit) radial vector.
 |
(2.50) |




Next: Loop Elements
Up: Curve Elements
Previous: Circular Region:
Contents
Darla Weiss
2000-02-13
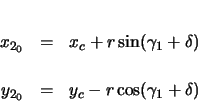
![]() , clothoid 2 must end with
, clothoid 2 must end with ![]() , and therefore begin at
, and therefore begin at ![]() , with non-zero curvature. The range of
, with non-zero curvature. The range of ![]() is depicted in figure 2.4.
is depicted in figure 2.4.