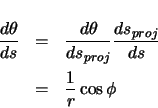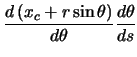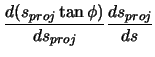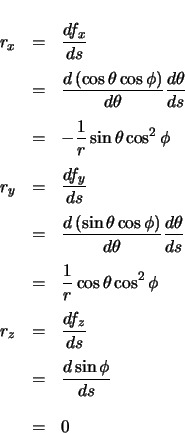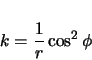Next: Clothoid 2:
Up: Curve Elements
Previous: Clothoid 1:
Contents
The azimuth angle at any point of the circular region is determined with the following.
The end of the first clothoid occurs when 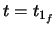 . This point is labeled
. This point is labeled
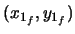 and is depicted in figure 2.4.
and is depicted in figure 2.4.
The center of the circular region can now be found from the following relationship.
The positions in the circular region are then determined with the following. Note that  is
calculated in the same manner as before, as it varies linearly with arclength along the curve.
is
calculated in the same manner as before, as it varies linearly with arclength along the curve.
Derivatives with respect to arclength will need to be taken to determine the remaining functions.
Since the position vector is expressed in terms of 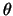 , the chain rule is applied.
, the chain rule is applied.
The forward vector is the derivative of the position vector with respect to arclength.
The radial vector is the derivative of the forward vector with respect to arclength.
The unit vector in the direction of the radial vector must be determined.
The curvature is the magnitude of the (non-unit) radial vector.
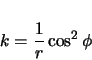 |
(2.40) |
Note the similarity of the above to equation 2.30. The curvature of a clothoid,
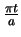 has been replaced by the curvature of a circle,
has been replaced by the curvature of a circle,  . The
. The  term exists in both curvature equations, due to the linearly varying elevation along the curve.
term exists in both curvature equations, due to the linearly varying elevation along the curve.




Next: Clothoid 2:
Up: Curve Elements
Previous: Clothoid 1:
Contents
Darla Weiss
2000-02-13
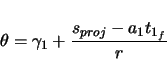
![]() . This point is labeled
. This point is labeled
![]() and is depicted in figure 2.4.
and is depicted in figure 2.4.
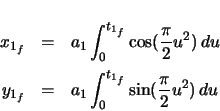
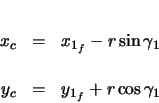
![]() , the chain rule is applied.
, the chain rule is applied.