All regions

The overhead view of the loop shown in figure 2.5 illustrates the loop as it has just been calculated, with a non-zero initial azimuth angle. As explained in section 2.1, the azimuth angle must be zero at the start of every element. This is required in order to guarantee slope continuity when the elements are joined. Since the loop has a non-zero initial azimuth angle, it must be rotated $-\alpha$ radians about the $z$ axis. This results in both the initial and final azimuth angles being zero.

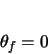$$\theta_{f} = 0$$ (2.83)

The rotation is performed as follows, where the subscript 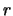$r$ stands for rotated, and the subscript 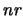$nr$ stands for non-rotated.

$$\begin{eqnarray*} x_{r} & = & x_{nr} \cos(-\alpha) - y_{nr} \sin(-\alpha) \\ ... ...& -x_{nr} \sin\alpha + y_{nr} \cos\alpha \\ z_{r} & = & z_{nr} \end{eqnarray*}$$

The rotation must be performed on the position vectors, forward vectors, and radial vectors. A more complete description of rotation transformations is given in appendix B.