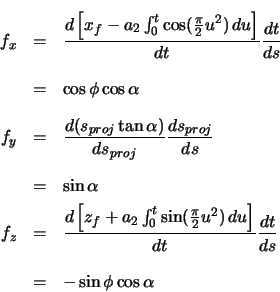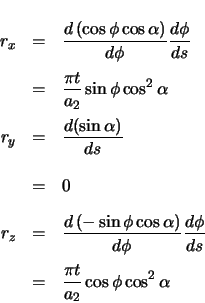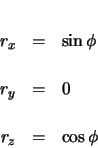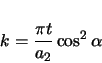Next: All Regions
Up: Corkscrew Elements
Previous: Circular Region:
Contents
The end of the corkscrew has zero curvature, and is where 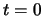 . Therefore,
. Therefore, 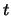 ranges from
ranges from
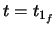 at the beginning of clothoid 2, to
at the beginning of clothoid 2, to 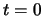 at the end of clothoid 2.
at the end of clothoid 2.
The vertical angle through clothoid 2 is found from the following.
The coordinates at the end of the corkscrew are found from the coordinates of the center of the
circular region of the corkscrew.
The position of all points along the clothoid can now be calculated relative to the zero curvature
end. The 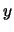 component is determined the same way as for the previous sections.
component is determined the same way as for the previous sections.
The position vector is now rotated downward 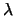 radians about the
radians about the  axis.
axis.
Derivatives with respect to arclength of the position vector must be taken. The required chain
rule relationships are first determined.
The forward vector is calculated as the derivative of the position vector with respect to arclength.
This vector is then rotated 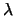 radians about the
radians about the  axis.
axis.
The radial vector is calculated as the derivative of the forward vector with respect to arclength.
The unit vector in the direction of the radial vector must be determined.
This vector is then rotated 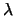 radians about the
radians about the  axis.
axis.
The curvature is the magnitude of the (non-unit) radial vector.
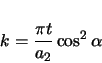 |
(2.113) |




Next: All Regions
Up: Corkscrew Elements
Previous: Circular Region:
Contents
Darla Weiss
2000-02-13
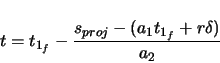
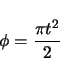
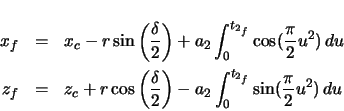
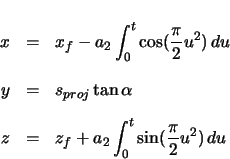
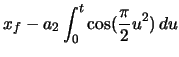
![$\displaystyle s_{proj} \tan\alpha \cos\lambda - \left[ z_{f} + a_{2} \ensuremath\int_{0}^{t} \sin(\frac{\pi}{2} u^{2})\,du \right] \sin\lambda$](img274.gif)
![$\displaystyle s_{proj} \tan\alpha \sin\lambda + \left[ z_{f} + a_{2} \ensuremath\int_{0}^{t} \sin(\frac{\pi}{2} u^{2})\,du \right] \cos\lambda$](img275.gif)