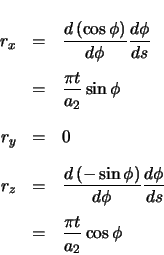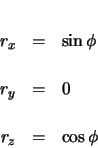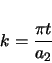Next: Connecting Elements to Create
Up: Joint Elements
Previous: Circular Region:
Contents
The end of the joint has zero curvature, and is where  . Therefore,
. Therefore, 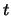 ranges from
ranges from 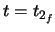 at the beginning of clothoid 2, to
at the beginning of clothoid 2, to 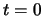 at the end of clothoid 2.
at the end of clothoid 2.
The vertical angle throughout clothoid 2 is found from the following.
The coordinates at the beginning of clothoid 2 are initially found by determining the endpoint of
the circular region. For the non-transformed (not yet negated and rotated) circle, this position is
found from the following.
If a downward joint is being calculated,  must be negated. This position vector is
then rotated
must be negated. This position vector is
then rotated 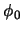 radians about the
radians about the 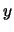 axis.
axis.
The position of clothoid 2 is determined by creating a clothoid which initially ends horizontally. The method used here is much like the method used for a curve.2.10 First, the end of the clothoid is determined. See figure 2.11.
Now the positions within the clothoid are determined relative to the endpoint.
If a downward joint is being calculated,  must be negated. The clothoid is then
rotated
must be negated. The clothoid is then
rotated  radians about the
radians about the 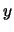 axis to line it up with the adjacent elements. It is then
translated to line up with the end of the circular region.
axis to line it up with the adjacent elements. It is then
translated to line up with the end of the circular region.
Derivatives with respect to arclength of the position vector must be taken. The required chain
rule relationships are first determined.
The forward vector is calculated by taking the derivative of the position vector as it was first
calculated. It will then be transformed in the same way as the position vector was, with the
exception of translations, which do not affect the forward and radial vectors.
The  coordinate is negated if a downward joint is being calculated. The vector is then rotated
coordinate is negated if a downward joint is being calculated. The vector is then rotated  radians about the
radians about the 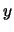 axis.
axis.
The radial vector is calculated as the derivative of the forward vector (with respect to arclength)
as it is initially calculated.
The unit vector in the direction of the radial vector must be determined.
The  coordinate is negated if a downward joint is being calculated. The vector is then rotated
coordinate is negated if a downward joint is being calculated. The vector is then rotated
 radians about the
radians about the 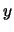 axis. The result will still be a unit vector, as rotation does not
alter magnitude.
axis. The result will still be a unit vector, as rotation does not
alter magnitude.
The curvature is the magnitude of the (non-unit) radial vector.
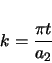 |
(2.146) |
2.10
Refer to section 2.1.2.




Next: Connecting Elements to Create
Up: Joint Elements
Previous: Circular Region:
Contents
Darla Weiss
2000-02-13

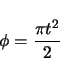
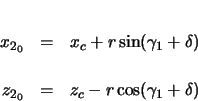
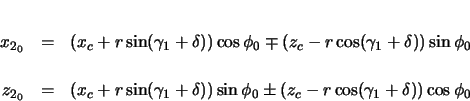

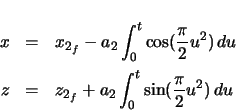
![$\displaystyle x_{2_{0}} + \left[ x_{2_{f}} - a_{2} \ensuremath\int_{0}^{t} \cos(\frac{\pi}{2} u^{2})\,du \right] \cos\phi_{f}$](img328.gif)
![$\displaystyle \mp \left[ z_{2_{f}} + a_{2} \ensuremath\int_{0}^{t} \sin(\frac{\pi}{2} u^{2})\,du \right] \sin\phi_{f}$](img329.gif)
![$\displaystyle z_{2_{0}} + \left[ x_{2_{f}} - a_{2} \ensuremath\int_{0}^{t} \cos(\frac{\pi}{2} u^{2})\,du \right] \sin\phi_{f}$](img330.gif)
![$\displaystyle \pm \left[ z_{2_{f}} + a_{2} \ensuremath\int_{0}^{t} \sin(\frac{\pi}{2} u^{2})\,du \right] \cos\phi_{f}$](img331.gif)

![\begin{eqnarray*}
f_{x} & = & \ensuremath \frac{d\left[ a_{1} x_{2_{f}} - a_{2}...
...du \right]}{dt} \ensuremath \frac{dt}{ds}
\\
& = & -\sin\phi
\end{eqnarray*}](img333.gif)