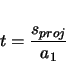
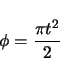
The projection of the corkscrew in the ![]() -
-![]() plane is determined by the Fresnel Integrals. The
plane is determined by the Fresnel Integrals. The ![]() coordinate varies linearly with the arclength of the corkscrew.
coordinate varies linearly with the arclength of the corkscrew.
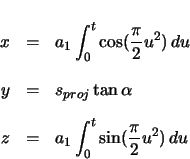
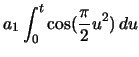 |
(2.84) | ||
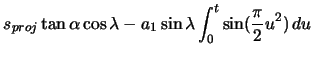 |
(2.85) | ||
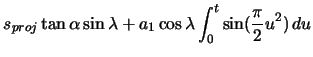 |
(2.86) |
The calculation of the forward and radial vectors can be performed two ways. The derivatives of the final position vector (with respect to arclength) may be taken, or the derivative may be taken before the rotation is made. The forward and radial vectors would then be rotated. The latter method will be used here, as it was for a curve.
The calculation of the forward and radial vectors is nearly identical to the calculation for a loop and a curve. An abbreviated description will be given here. For a more complete description, refer to section 2.1.2.
Derivatives of the position vector with respect to arclength must be taken. The required chain rule relationships are first determined.
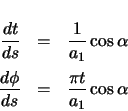
The forward vector is calculated as the derivative of the position vector with respect to arclength.
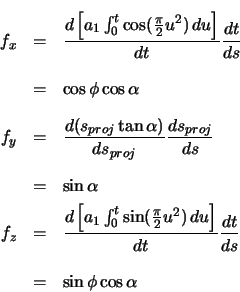
| (2.87) | |||
| (2.88) | |||
| (2.89) |
The radial vector is calculated as the derivative of the forward vector with respect to arclength.
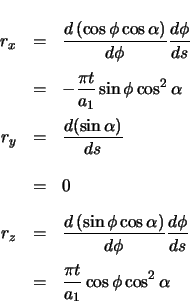
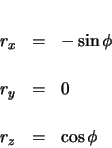
| (2.90) | |||
| (2.91) | |||
| (2.92) |
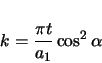 |
(2.93) |