



Next: Specifications
Up: Introduction
Previous: Roller Coaster Basics
Contents
Notation
Before proceeding with any mathematical derivations, an introduction to the notation being used
may be helpful. When new key terms are introduced, they will be written in italics.
Parameters are constants that geometrically describe the track and its elements.
Each element type requires different parameters to be specified. Variables change along
the track. Since the car is constrained to move along the track, this is a single degree of freedom
system, with the DOF being the distance along the track. This distance is the independent
variable. Functions vary along the track. All functions are dependent on the independent
variable. The term quantities will be used to encompass parameters, variables, and functions,
essentially referring to all numeric quantities.
Vectors will be represented in boldface,  ; while scalars will be represented in plain
font,
; while scalars will be represented in plain
font, 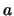 . A unit vector will be represented as a vector with a hat over it,
. A unit vector will be represented as a vector with a hat over it,
 . In this
way, the types of quantities used can easily be distinguished from one another.
. In this
way, the types of quantities used can easily be distinguished from one another.
Three coordinate systems will be used in this research. All are right-handed, orthogonal systems.
See figure 1.3.
Figure 1.3: Coordinate Systems.
The track segment shown is a left-hand upward curve followed by an upward straight section. The curve begins at the origin of the global coordinate system,
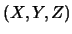 ,
since it is the first element of the track. The forward vector is labeled
,
since it is the first element of the track. The forward vector is labeled
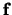 ,
and the radial vector
,
and the radial vector
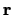 .
Note that the radial vector has no vertical component. The local coordinate system shown,
.
Note that the radial vector has no vertical component. The local coordinate system shown,
 starts at the beginning of the straight section.
starts at the beginning of the straight section.

|
- Global
- An inertial coordinate system is established, denoted in capitals as
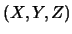 , and whose axes are in the
, and whose axes are in the
 directions. The
directions. The  direction is the vertical direction, and is perpendicular to the surface of the earth. The
origin of the global coordinate system is placed at the station, where the track begins. The initial
track direction is along the
direction is the vertical direction, and is perpendicular to the surface of the earth. The
origin of the global coordinate system is placed at the station, where the track begins. The initial
track direction is along the 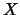 axis. All quantities dealing with the global coordinate system will
be expressed in capitals.
axis. All quantities dealing with the global coordinate system will
be expressed in capitals.
- Local
- An inertial coordinate system is created for each new element that is added.
The coordinates are represented in lower case by
 , with the corresponding axes in the
standard
, with the corresponding axes in the
standard
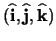 directions. The origin of the local coordinate system is
placed at the beginning of the particular track element being described. The local coordinate
system is aligned such that the
directions. The origin of the local coordinate system is
placed at the beginning of the particular track element being described. The local coordinate
system is aligned such that the  axis is parallel to the
axis is parallel to the  axis. The initial track direction is in
the
axis. The initial track direction is in
the  -
- plane.1.3
plane.1.3
- Car-Fixed
- A non-inertial coordinate system is created with the origin affixed to the
center of gravity of the car. The unit vectors are represented by
 1.4, which represent the forward and radial
vectors.1.5 The forward vector points in the direction the car is
moving, while the radial direction points toward the center of curvature.
1.4, which represent the forward and radial
vectors.1.5 The forward vector points in the direction the car is
moving, while the radial direction points toward the center of curvature.
The distance a car has traveled along the track will be denoted as 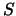 , while the distance a car
has traveled into an element will be denoted as
, while the distance a car
has traveled into an element will be denoted as  . The total length of an element is denoted by
either
. The total length of an element is denoted by
either 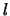 or
or 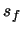 . Note that the function
. Note that the function  is dependent on the independent variable
is dependent on the independent variable 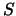 and the parameters
and the parameters 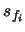 of all previous elements.
of all previous elements.
Figure 1.4: Azimuth and Vertical Angles.
The azimuth is represented by
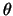 ,
while
,
while
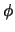 represents the vertical angle. The vector
represents the vertical angle. The vector
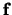 is the forward vector, and
is the forward vector, and
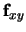 is the projection of the forward vector in the
is the projection of the forward vector in the
 -
-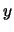 plane.
plane.

|
The azimuth angle is denoted as 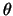 , and is defined as the angle between the projection of
the forward vector in the
, and is defined as the angle between the projection of
the forward vector in the  -
-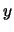 plane and the
plane and the  axis. Refer to figure 1.4. The element will be created such that the azimuth angle at the beginning of an element is zero. The azimuth angle at the end of an element is denoted as
axis. Refer to figure 1.4. The element will be created such that the azimuth angle at the beginning of an element is zero. The azimuth angle at the end of an element is denoted as  .
.
The vertical angle is denoted by 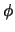 , and is defined as the angle between the forward direction
and the
, and is defined as the angle between the forward direction
and the  -
-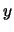 plane. Refer again to figure 1.4. The vertical angles at the
beginning and end of an element are denoted as
plane. Refer again to figure 1.4. The vertical angles at the
beginning and end of an element are denoted as 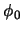 and
and  , respectively.
, respectively.
In dynamic calculations, the derivative with respect to time, as in
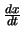 , is used frequently
and is denoted simply as
, is used frequently
and is denoted simply as 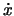 .
.
1.3
Note that the initial direction may or may not be along the  -axis,
due to the possibility of a non-zero vertical angle (described below). However, the initial
-axis,
due to the possibility of a non-zero vertical angle (described below). However, the initial 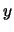 value will always be zero.
value will always be zero.
1.4
A third vector would be defined as the cross product of
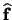 and
and
 ; however, this
vector is not needed in the calculations presented here.
; however, this
vector is not needed in the calculations presented here.
1.5
These correspond to the tangential and normal vectors of the Frenet frame:
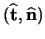 [11].
[11].




Next: Specifications
Up: Introduction
Previous: Roller Coaster Basics
Contents
Darla Weiss
2000-02-13
![]() ; while scalars will be represented in plain
font,
; while scalars will be represented in plain
font, ![]() . A unit vector will be represented as a vector with a hat over it,
. A unit vector will be represented as a vector with a hat over it,
![]() . In this
way, the types of quantities used can easily be distinguished from one another.
. In this
way, the types of quantities used can easily be distinguished from one another.

![]() , while the distance a car
has traveled into an element will be denoted as
, while the distance a car
has traveled into an element will be denoted as ![]() . The total length of an element is denoted by
either
. The total length of an element is denoted by
either ![]() or
or ![]() . Note that the function
. Note that the function ![]() is dependent on the independent variable
is dependent on the independent variable ![]() and the parameters
and the parameters ![]() of all previous elements.
of all previous elements.
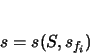

![]() , and is defined as the angle between the projection of
the forward vector in the
, and is defined as the angle between the projection of
the forward vector in the ![]() -
-![]() plane and the
plane and the ![]() axis. Refer to figure 1.4. The element will be created such that the azimuth angle at the beginning of an element is zero. The azimuth angle at the end of an element is denoted as
axis. Refer to figure 1.4. The element will be created such that the azimuth angle at the beginning of an element is zero. The azimuth angle at the end of an element is denoted as ![]() .
.


![]() , is used frequently
and is denoted simply as
, is used frequently
and is denoted simply as ![]() .
.