Integration of the Equations of Motion

The system is described by a single degree of freedom, $S$, the distance along the track. However, the free body diagrams give the second derivative of $S$, the acceleration. This requires both the position and velocity to be calculated as state variables, since the integration routine to be used will solve for the derivative of the state variables. Thus, the acceleration will be calculated from the integration routine, and used with the equations produced from the free body diagram to calculate the forces on the car. The state variables are intoduced below.

$$s_{1} = S$$ (3.4)

$$s_{2} = v$$ (3.5)

A Runge-Kutta-Fehlburg integration routine will be used to solve for the state variables. The required derivatives of the state variables are shown here.

$$\begin{eqnarray*} \dot{s_{1}} & = & v \\ & = & s_{2} \\ \dot{s_{2}} & = & a \end{eqnarray*}$$

The value of $a$ is calculated by means of the free body diagram presented in section 3.1. The component of the forces and accelerations in the $\ensuremath \mathbf{\widehat{f}}$ direction are equated.

$$\begin{eqnarray*} \sum F_{\ensuremath \mathbf{\widehat{f}}} & = & ma_{\ensurema... ...mathbf{\widehat{r}} \cdot \ensuremath \mathbf{\widehat{f}} ) \\ \end{eqnarray*}$$

Recall that $\ensuremath \mathbf{\widehat{r}}$ and $\ensuremath \mathbf{\widehat{u}}$ are perpendicular to $\ensuremath \mathbf{\widehat{f}}$. Evaluating the dot products results in the following.

$$- \left( C_{a} v^{2} + C_{s} F_{s} + C_{c} \right) - mgf_{z} = ma$$ (3.6)

Equation 3.6 is now solved for $a$.

$$a = -\frac{1}{m} \left( C_{a} v^{2} + C_{s} F_{s} + C_{c} \right) - gf_{z}$$ (3.7)

The result shows that $F_{s}$ must also be calculated. Further analysis of the free body diagram is made. First the components of the forces and accelerations in the $\ensuremath \mathbf{\widehat{r}}$ direction are found.

$$\begin{eqnarray*} \sum F_{\ensuremath \mathbf{\widehat{r}}} & = & ma_{\ensurema... ...mathbf{\widehat{r}} \cdot \ensuremath \mathbf{\widehat{r}} ) \\ \end{eqnarray*}$$

Evaluation of the dot product results in the following.

$$F_{s} \left( u_{x}r_{x} + u_{y}r_{y} + u_{z}r_{z} \right) - mgr_{z} = mkv^{2}$$ (3.8)

The components of forces and accelerations in the $\ensuremath \mathbf{\widehat{u}}$ direction are now determined.

$$\begin{eqnarray*} \sum F_{\ensuremath \mathbf{\widehat{u}}} & = & ma_{\ensurema... ...t{r}} \cdot \ensuremath \mathbf{\widehat{u}} ) \hspace{.4in} \\ \end{eqnarray*}$$

The dot product is then evaluated.

$$F_{s} - mgu_{z} = mkv^{2} \left( r_{x}u_{x} + r_{y}u_{y} + r_{z}u_{z} \right) \hspace{.4in}$$ (3.9)

And finally, the components in the $\ensuremath \mathbf{\widehat{k}}$ direction are found.

$$\begin{eqnarray*} \sum F_{\ensuremath \mathbf{\widehat{k}}} & = & ma_{\ensurema... ...mathbf{\widehat{r}} \cdot \ensuremath \mathbf{\widehat{k}} ) \\ \end{eqnarray*}$$

The dot product is evaluated to produce equation 3.10.

$$F_{s}u_{z} - \left( C_{a} v^{2} + C_{s} F_{s} + C_{c} \right)f_{z} -mg = maf_{z} + mkv^{2}r_{z}$$ (3.10)

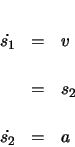
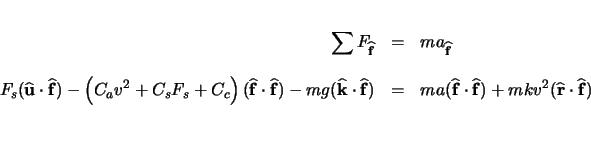
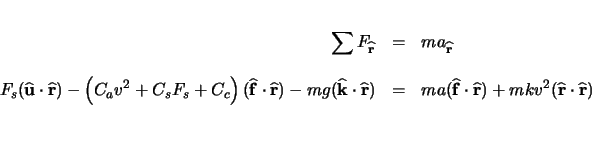
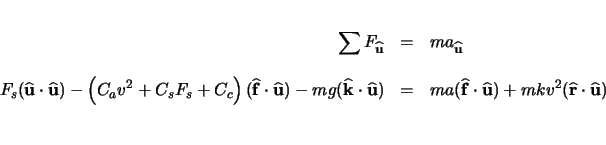
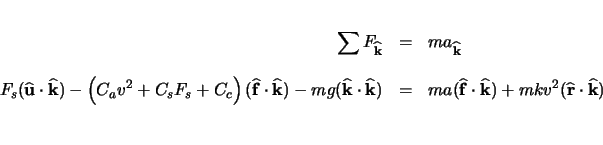
Equations 3.6, 3.8, 3.9, and 3.10 can be combined to determine $F_{s}$. First, equations 3.8 and 3.9 are combined to eliminate $\ensuremath \mathbf{\widehat{r}} \cdot \ensuremath \mathbf{\widehat{u}}$. The result is then combined with equation 3.10 to eliminate $u_{z}$. Finally, equation 3.6 was used to eliminate $a$. The resulting seat force equation is shown here.

$$F_{s} = \pm \sqrt{ (mg)^{2} + 2(mg)(mkv^{2})r_{z} + (mkv^{2})^{2} - (mgf_{z})^{2} }$$ (3.11)

Many quantities in the equations for $a$ and $F_{s}$ are geometric variables, and depend on which element the car is traveling in. These include $k$, $\ensuremath \mathbf{\widehat{f}}$, and $\ensuremath \mathbf{\widehat{r}}$. The independent variable, $S$, is used to calculate the distance into the current element, as shown in equation 3.12. Let $s_{i}$ represent the distance into the $i^{th}$ element, and let $s_{f_{i}}$ represent the total length of that element.

$$s_{i} = S - \sum_{j=1}^{i-1} s_{f_{i}}$$ (3.12)

This distance is then used to determine the geometric quantities using the methods discussed in chapter 2.

The values of the state variables come from the integration routine. The values of $S$ and $v$ used in the calculation of the current $a$ and $F_{s}$ are those from the previous iteration. The time step used should be small, as a smaller time step will result in more accurate results. The limiting factor in this will typically be the computer on which the program is run. Many data values are created, and a smaller time step requires more calculations to be performed and more memory to store the results.

A discussion of the Runge-Kutta-Fehlburg method can be found in many numerical methods texts. C code is also available to perform the routine[13].