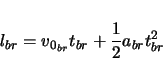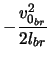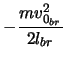Next: Dynamic Results
Up: Special Sections
Previous: Lift Hill
Contents
The brake run is the last portion of a roller coaster. It is where brakes slow the train to a stop, allowing passengers to exit and new passengers to board. For the purposes of this research, the brakes are assumed to provide a constant force such that the train will be slowed with constant deceleration from the time it enters the brake run to the time it reaches the station. The brake force only acts in the tangential direction.
The speed at the end of the brake run should be zero. The speed at the beginning of the brake run is 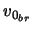 . The distance the car travels over the brakes is
. The distance the car travels over the brakes is 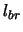 .
.
The deceleration and brake force can now be found.




Next: Dynamic Results
Up: Special Sections
Previous: Lift Hill
Contents
Darla Weiss
2000-02-13
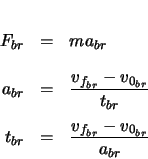
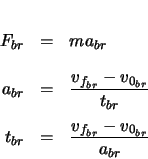
![]() . The distance the car travels over the brakes is
. The distance the car travels over the brakes is ![]() .
.