The desired results of the simulation are the position, speed, and acceleration of the roller coaster car as it traverses the track, as well as the magnitude of the seat force, the up direction, and position of the rails.
The position and speed come directly from the integration routine and are shown in equations 3.4-3.5. The acceleration is determined from equation 3.7, and the seat force is determined from equation 3.11.
To find the components of the up vector, it is necessary to return to the free body diagram shown
in figure 3.1. The components in the
![]() direction is now found.
direction is now found.
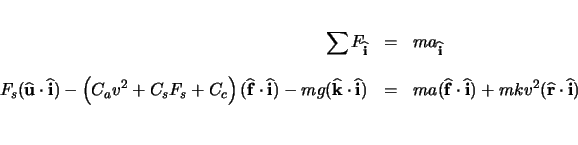
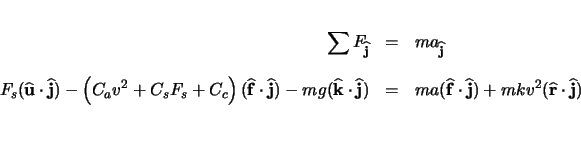
From equations 3.15, 3.16, and 3.10 we can solve for the components of
![]() .
.
![\begin{eqnarray*}
u_{x} & = & \frac{1}{F_{s}} \left[ maf_{x} + \left( C_{a}v^{2...
...} + C_{s}F_{s} + C_{c}
\right) f_{z} + mkv^{2}r_{z} + mg \right]
\end{eqnarray*}](img420.gif)
The position of the rails can now be found. First, the value of ![]() is found from the independent variable
is found from the independent variable ![]() , and equation 3.12. The techniques presented in chapter 2 are then used to determine the position vector,
, and equation 3.12. The techniques presented in chapter 2 are then used to determine the position vector, ![]() . Then the lateral vector, the direction toward the right side of the car, is found from
. Then the lateral vector, the direction toward the right side of the car, is found from
![]() . The track gage,
. The track gage, ![]() , and distance from the center of gravity of the car to the rails,
, and distance from the center of gravity of the car to the rails, ![]() , are specified by the track designer. The position of the left rail is denoted as
, are specified by the track designer. The position of the left rail is denoted as ![]() , while the position of the right rail is
, while the position of the right rail is ![]() .
.
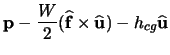 |
(3.17) | ||
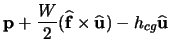 |
(3.18) |