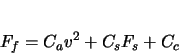Wind

The wind can have a significant effect on the dynamics of a roller coaster[5]. The wind affects the speed of a roller coaster in a similar manner as aerodynamic drag. Complexities involved in calculating the effect of the wind include its variation with the height of the track and its generally unpredictable behavior.

Unfortunately, the resources were not available for this research to create a highly accurate friction model. However, the model presented is the same as the one commonly used for road vehicles, which has been known to produce very good results. Special concerns for roller coasters are not dealt with by this model, such as the forces on the different sets of wheels. Experiments would need to be performed, requiring access to a roller coaster car and track. Since these facilities were not available, a simplified model will be described as follows.

$$F_{f} = C_{a}v^{2} + C_{s}F_{s} + C_{c}$$ (3.2)

The value of $C_{a}$ is the aerodynamic coefficient, in general given by $\frac{1}{2} \rho A_{f}C_{d}$; but the flexibility exists to set the value to be whatever is desired, so that a wind effect may be added, or anything else that is required. The value of $C_{s}$ is the coefficient to be multiplied by the seat force. This may simply be the rolling friction coefficient, or may be more complex. Similarly, $C_{c}$ may be a lubricant drag coefficient, or may also include any other constant value that is needed to properly model the friction.

The model presented here provides the general framework of a friction model, accounting for an aerodynamic term, a force dependent term, and a force independent term. The specific values used in this model are implementation dependent, and may vary with each roller coaster. The model is intended to be complete enough, yet flexible enough, to allow a designer with a knowledge of the appropriate friction coefficients to be able to utilize them.

With the friction model expressed as equation 3.2, the force balance of equation 3.1 can be rewritten as follows.

$$F_{s} \ensuremath \mathbf{\widehat{u}} - \left( C_{a} v^{2}... ...mathbf{\widehat{f}} + mkv^{2} \ensuremath \mathbf{\widehat{r}}$$ (3.3)