



Next: Axis Calculations
Up: Elements
Previous: All regions
Contents
Corkscrew Elements
A corkscrew is another element used to turn riders upside down. In order to understand a
corkscrew, consider this analogy. Imagine wrapping a section of track around a cylinder. Now
tilt the cylinder slightly downward, so the average kinetic energy lost to friction can be recovered
from potential energy[6]. If you look at the track along the axis of the cylinder, it
will appear circular. If you look at it from the side, it will appear sinusoidal. This is the initial
shape considered for a corkscrew: a helix with a downward sloping axis. But in order to
maintain continuous curvature, modifications were required. The ``circle'' observed from the end
must be clothoidal entering and exiting the corkscrew; therefore, the end view of a corkscrew
greatly resembles that of a clothoid loop.
The circular/clothoidal plane is the  -
- plane, while the sinusoid lies in the
plane, while the sinusoid lies in the 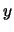 -
- plane
along with the central axis. A corkscrew is described by six parameters, described below and
illustrated in figure 2.7.
plane
along with the central axis. A corkscrew is described by six parameters, described below and
illustrated in figure 2.7.
Figure 2.7: Corkscrew Element Parameters.
The figure on the left shows the projection of the corkscrew in the
 -
- plane, illustrating the circular and clothoidal regions. Note the resemblance to a loop element. The figure on the right shows the side view of the corkscrew, along with its central axis. There is no axis tilt in the corkscrew depicted in these figures.
plane, illustrating the circular and clothoidal regions. Note the resemblance to a loop element. The figure on the right shows the side view of the corkscrew, along with its central axis. There is no axis tilt in the corkscrew depicted in these figures.

|
- direction
- The direction of the corkscrew. Either clockwise or counter-clockwise.
- number of loops

- The number of inversions in the corkscrew.
- radius

- The minimum radius of the corkscrew. This is the constant radius of
curvature in the helical region of the corkscrew. (
 )
)
- clothoid angle

- Clothoid 1 is the region in which the curvature varies
from zero to
 . In clothoid 2 it varies back from
. In clothoid 2 it varies back from  to zero. For the corkscrew, all
parameters describing these clothoids are identical. The vertical angle change experienced by the
car as it traverses these clothoids is
to zero. For the corkscrew, all
parameters describing these clothoids are identical. The vertical angle change experienced by the
car as it traverses these clothoids is  .2.6 (
.2.6 (
 )
)
- chord angle

- An angle related to, but not the same as, the pitch of a helix. Depicted in the figure on the right, and described in greater detail below. (
 )
)
- downward tilt

- The downward slope of the central axis. The reason for the downward tilt is so that some of the kinetic energy lost to friction can be regained from potential energy. (
 )
)
The angle of the circular region is found from the number of loops and the clothoid angle.
The length of the projection in the  -
- plane is found from the equations for the arclength of
a clothoid and of a circle.
plane is found from the equations for the arclength of
a clothoid and of a circle.
To develop a corkscrew, the central axis is first calculated. The points of the corkscrew are then
calculated relative to the axis, and rotated downward 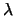 radians, the tilt of the axis. The
distance along the axis,
radians, the tilt of the axis. The
distance along the axis,  is specified such that it varies linearly with
is specified such that it varies linearly with 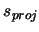 , the
projected arclength in the
, the
projected arclength in the  -
- plane.
plane.
2.6
The vertical angle change expressed here is the angle before the downward 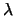 rotation, which is explained in detail later.
rotation, which is explained in detail later.
Subsections




Next: Axis Calculations
Up: Elements
Previous: All regions
Contents
Darla Weiss
2000-02-13
![]() -
-![]() plane, while the sinusoid lies in the
plane, while the sinusoid lies in the ![]() -
-![]() plane
along with the central axis. A corkscrew is described by six parameters, described below and
illustrated in figure 2.7.
plane
along with the central axis. A corkscrew is described by six parameters, described below and
illustrated in figure 2.7.



![]() radians, the tilt of the axis. The
distance along the axis,
radians, the tilt of the axis. The
distance along the axis, ![]() is specified such that it varies linearly with
is specified such that it varies linearly with ![]() , the
projected arclength in the
, the
projected arclength in the ![]() -
-![]() plane.
plane.