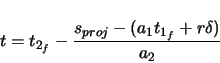Clothoid 2: $(a_{1}t_{1_{f}} + r \delta \leq s_{proj} \leq l_{proj} )$

The coordinates at the beginning of clothoid 2 are found from the coordinates of the center of the curve.

$$\begin{eqnarray*} x_{2_{0}} & = & x_{c} + r \sin(\gamma_{1} + \delta) \\ y_{2_{0}} & = & y_{c} - r \cos(\gamma_{1} + \delta) \end{eqnarray*}$$

The end of the curve element has zero curvature. Since clothoids have zero curvature when 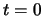$t=0$, clothoid 2 must end with 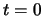$t=0$, and therefore begin at 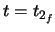$t=t_{2_{f}}$, with non-zero curvature. The range of 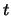$t$ is depicted in figure 2.4.

$$t = t_{2_{f}} - \frac{s_{proj} - (a_{1}t_{1_{f}} + r \delta)}{a_{2}}$$

Clothoid 2 is initially created ending at horizontal, as seen in the figure. The azimuth angle along the clothoid is found from the value of 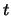$t$ given above and from equation A.7.

$$\theta = \frac{\pi t^{2}}{2}$$

The location of the end of the clothoid is calculated, $(x_{2_{f}},y_{2_{f}})$, and can be seen in the figure after the clothoid's translation to begin at its starting point, $(x_{2_{0}},y_{2_{0}})$.

$$\begin{eqnarray*} x_{2_{f}} & = & a_{2} \ensuremath\int_{0}^{t_{2_{f}}} \cos(\f... ...2} \ensuremath\int_{0}^{t_{2_{f}}} \sin(\frac{\pi}{2} u^{2})\,du \end{eqnarray*}$$

The coordinates of all points along the clothoid are then calculated from the endpoint of the clothoid, $(x_{2_{f}},y_{2_{f}})$.

$$\begin{eqnarray*} x & = & x_{2_{f}} - a_{2} \ensuremath\int_{0}^{t} \cos(\frac{... ...}} + a_{2} \ensuremath\int_{0}^{t} \sin(\frac{\pi}{2} u^{2})\,du \end{eqnarray*}$$

The clothoid is then rotated $\theta_{f}$ radians about the $z$ axis to line up the azimuth angle at the beginning of clothoid 2 with the angle at the end of the circular region. Appendix B discusses rotation transformations in detail. Clothoid 2 is translated to begin at $(x_{2_{0}},y_{2_{0}})$ after the rotation is complete.

$$x = x_{2_{0}} + \left( x_{2_{f}} - a_{2} \ensuremath\int_{0}^{t} \cos(\frac{\pi}{2} u^{2})\,du \right) \cos\theta_{f}$$

$$- \left( y_{2_{f}} + a_{2} \ensuremath\int_{0}^{t} \sin(\frac{\pi}{2} u^{2})\,du \right) \sin\theta_{f}$$ (2.41)

$$y = y_{2_{0}} + \left( x_{2_{f}} - a_{2} \ensuremath\int_{0}^{t} \cos(\frac{\pi}{2} u^{2})\,du \right) \sin\theta_{f}$$

$$+ \left( y_{2_{f}} + a_{2} \ensuremath\int_{0}^{t} \sin(\frac{\pi}{2} u^{2})\,du \right) \cos\theta_{f}$$ (2.42)

$$z = s_{proj} \tan\phi$$ (2.43)

The calculation of the forward and radial vectors can be performed in two ways. The derivatives of the final position vector with respect to arclength may be taken, or the derivative may be taken before the rotation is made. The forward and radial vectors would then be rotated. The second approach will be used here.

The calculation of the derivatives is nearly identical to the calculation in clothoid 1. An abbreviated description will be shown here.

The required chain rule relationships are first determined.

$$\begin{eqnarray*} \ensuremath \frac{dt}{ds} & = & -\frac{1}{a_{2}} \cos\phi \\ ... ...nsuremath \frac{d\theta}{ds} & = & -\frac{\pi t}{a_{2}} \cos\phi \end{eqnarray*}$$

The forward vector is initially determined as the derivative with respect to arclength of the position vector before it is rotated.

$$\begin{eqnarray*} f_{x} & = & \ensuremath \frac{d\left[ x_{2_{f}} - a_{2} \ensu... ...s_{proj}} \ensuremath \frac{ds_{proj}}{ds} \\ & = & \sin\phi \end{eqnarray*}$$

This vector will now be rotated $\theta_{f}$ radians about the $z$ axis.

$$f_{x} = (\cos\theta \cos\phi)\cos\theta_{f} + (\sin\theta \cos\phi)\sin\theta_{f}$$ (2.44)

$$f_{y} = (\cos\theta \cos\phi)\sin\theta_{f} - (\sin\theta \cos\phi)\cos\theta_{f}$$ (2.45)

$$f_{z} = \sin\phi$$ (2.46)

The radial vector is initially determined as the derivative of the forward vector with respect to arclength, before its rotation.

$$\begin{eqnarray*} r_{x} & = & \ensuremath \frac{d\left( \cos\theta \cos\phi \ri... ...\\ r_{z} & = & \ensuremath \frac{d(\sin\phi)}{ds} \\ & = & 0 \end{eqnarray*}$$

The unit vector in the direction of the radial vector must be determined.

$$\begin{eqnarray*} r_{x} & = & \sin\theta \\ r_{y} & = & \cos\theta \\ r_{z} & = & 0 \end{eqnarray*}$$

This vector will now be rotated $\theta_{f}$ radians about the $z$ axis.

$$r_{x} = \sin\theta \cos\theta_{f} - \cos\theta \sin\theta_{f}$$ (2.47)

$$r_{y} = \sin\theta \sin\theta_{f} + \cos\theta \cos\theta_{f}$$ (2.48)

$$r_{z} = 0$$ (2.49)

The curvature is the magnitude of the (non-unit) radial vector.

$$k = \frac{\pi t}{a_{2}} \cos^{2}\phi$$ (2.50)