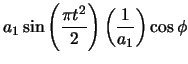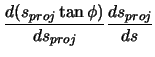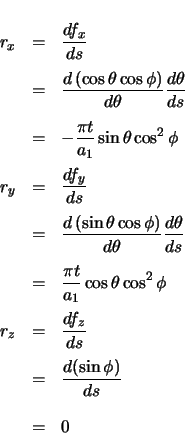Next: Circular Region:
Up: Curve Elements
Previous: Curve Elements
Contents
The variable 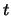 is used for clothoid calculations; however,
is used for clothoid calculations; however, 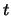 is actually a function of the
projected arclength,
is actually a function of the
projected arclength, 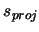 . In this way,
. In this way, 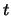 is used both as a function and as a variable.
Since
is used both as a function and as a variable.
Since 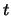 is a function of
is a function of 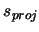 , which is itself a function of
, which is itself a function of  , which is a function of
, which is a function of 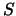 ,
, 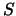 is ultimately the independent variable of all functions, as discussed in section 1.2.
is ultimately the independent variable of all functions, as discussed in section 1.2.
The equation of arclength of a clothoid is used to determine 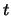 .
.
The azimuth angle along the curve is found from the value of 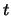 , using equation A.7.
, using equation A.7.
The projection of the curve in the  -
-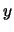 plane is determined by the Fresnel Integrals, which are described in appendix A. These integrals, when multiplied by the scaling factor
plane is determined by the Fresnel Integrals, which are described in appendix A. These integrals, when multiplied by the scaling factor 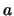 , will produce the coordinates of the points on a clothoid. The
, will produce the coordinates of the points on a clothoid. The  coordinates of the curve vary linearly with the arclength along the curve.
coordinates of the curve vary linearly with the arclength along the curve.
Derivatives with respect to arclength will need to be taken to determine the remaining functions.
Since the position vector is expressed in terms of 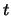 , the chain rule is applied. The chain rule
will also be applied to quantities expressed in terms of
, the chain rule is applied. The chain rule
will also be applied to quantities expressed in terms of 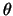 , so the required relationships are
developed here.
, so the required relationships are
developed here.
The forward vector is the derivative of the position vector with respect to arclength.
The radial vector is the derivative of the forward vector with respect to arclength.
The unit vector in the direction of the radial vector must be determined.
The curvature is the magnitude of the (non-unit) radial vector.
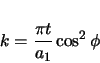 |
(2.30) |
For a curve with no elevation change, equation 2.30 reduces to
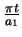 , which is the equation for the curvature of a planar clothoid.2.4 The only difference in curvature between a two-dimensional curve and a three-dimensional curve is the
, which is the equation for the curvature of a planar clothoid.2.4 The only difference in curvature between a two-dimensional curve and a three-dimensional curve is the  term, which has a constant value. This simple result is due to the method of linearly stretching the two-dimensional curve to create the three-dimensional element, as explained in section 1.4.
term, which has a constant value. This simple result is due to the method of linearly stretching the two-dimensional curve to create the three-dimensional element, as explained in section 1.4.
2.4
This is shown toward the beginning of this section and in appendix A.




Next: Circular Region:
Up: Curve Elements
Previous: Curve Elements
Contents
Darla Weiss
2000-02-13
![]() .
.
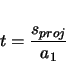

![]() -
-![]() plane is determined by the Fresnel Integrals, which are described in appendix A. These integrals, when multiplied by the scaling factor
plane is determined by the Fresnel Integrals, which are described in appendix A. These integrals, when multiplied by the scaling factor ![]() , will produce the coordinates of the points on a clothoid. The
, will produce the coordinates of the points on a clothoid. The ![]() coordinates of the curve vary linearly with the arclength along the curve.
coordinates of the curve vary linearly with the arclength along the curve.
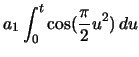
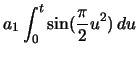
![]() , the chain rule is applied. The chain rule
will also be applied to quantities expressed in terms of
, the chain rule is applied. The chain rule
will also be applied to quantities expressed in terms of ![]() , so the required relationships are
developed here.
, so the required relationships are
developed here.
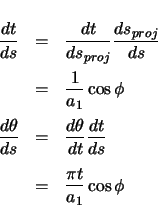
![$\displaystyle \ensuremath \frac{d\left[ a_{1} \ensuremath\int_{0}^{t} \cos(\frac{\pi}{2} u^{2})\,du \right]}{dt} \ensuremath \frac{dt}{ds}$](img141.gif)

![$\displaystyle \ensuremath \frac{d\left[ a_{1} \ensuremath\int_{0}^{t} \sin(\frac{\pi}{2} u^{2})\,du \right]}{dt} \ensuremath \frac{dt}{ds}$](img145.gif)